1. K-Means
- Expectation과 Maximization을 중심점 값이 최적값으로 고정될 때까지 반복
- 클러스터링으로 군집을 모으고 가장 각 클러스터에서 가장 중요한 값을 토픽으로 찾는다.
2. 실습
1) 랜덤 좌표값, 랜덤 중심 좌표값 생성
# K-Means
# rnk, muk(random) => Parameter, K => HypterParamater
# data = point = instance => Random(N)
from random import randrange
K = 3
N = 100 #[[?, ?], [], []]
centroid = list()
for i in range(K): # 랜덤 중심점 좌표 K개 만큼 생성
centroid.append((randrange(1, 100), randrange(1, 100)))
data = list()
for i in range(N): # 랜덤 좌표 N개 만큼 생성
data.append((randrange(1, 100), randrange(1, 100)))
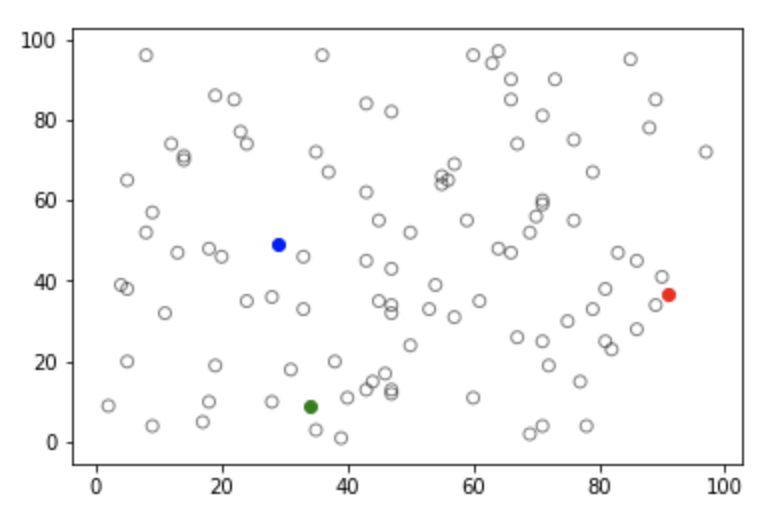
2) 그리기
import matplotlib.pyplot as plt
colorMap = ['r', 'g', 'b', 'k']
for _ in data:
plt.scatter(_[0], _[1], facecolor='none', alpha=.5, edgecolor=colorMap[-1])
for i, _ in enumerate(centroid):
plt.scatter(_[0], _[1], color=colorMap[i])
plt.show()
3) 두 점 간의 거리, 각도 계산
from math import sqrt
def distance(x1, x2):
return sqrt((x1[0]-x2[0]) ** 2 + (x1[1]-x2[1])**2)
def angle(x1, x2):
return (x1[0]*x2[0] + x1[1]*x2[1]) / (distance(x1,(0,0)) * (distance(x2,(0,0))))
4) 각 좌표의 클러스터링 집합 결정
# EM Algorithm
# E-Expectation = rnk assignement => distance
# M-Maximization = centroid update
def expectation(x, c):
candidates = list()
rnk = list() # => [0,0,1]
for _ in c:
candidates.append(distance(x, _))
return candidates.index(min(candidates))
5) 새로운 중심 좌표 값 계산
# 클러스터 내 데이터 좌표의 합 / 클러스터 내 데이터 갯수
def maximization(X):
return (sum([x[0] for x in X])/len(X), sum([x[1] for x in X])/len(X))
6) 클러스터링 해보기
rnk = list(list(0 for _ in range(K)) for _ in range(N)) # 빈 공간 생성(각 클러스터에 소속 가능한 갯수만큼 초기값 0
for i in range(N):
j = expectation(data[i], centroid)
rnk[i][j] = 1
rnk

7) 새로운 리스트 만들고 재귀적으로 실행
rnk = list(list(0 for _ in range(K)) for _ in range(N)) # 빈 공간 생성(각 클러스터에 소속 가능한 갯수만큼 초기값 0
for i in range(N):
j = expectation(data[i], centroid)
rnk[i][j] = 1
for k in range(K):
X = [data[i] for i in range(N) if rnk[i][k]]
print(centroid[k])
centroid[k] = maximization(X)
print(centroid[k])
print()
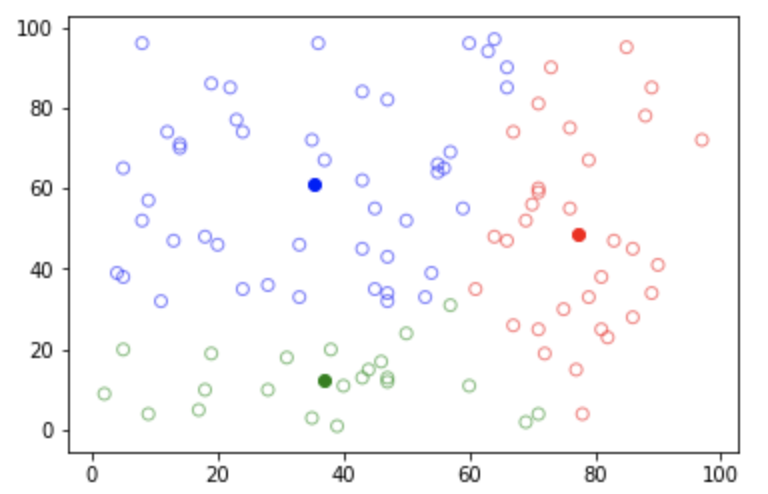
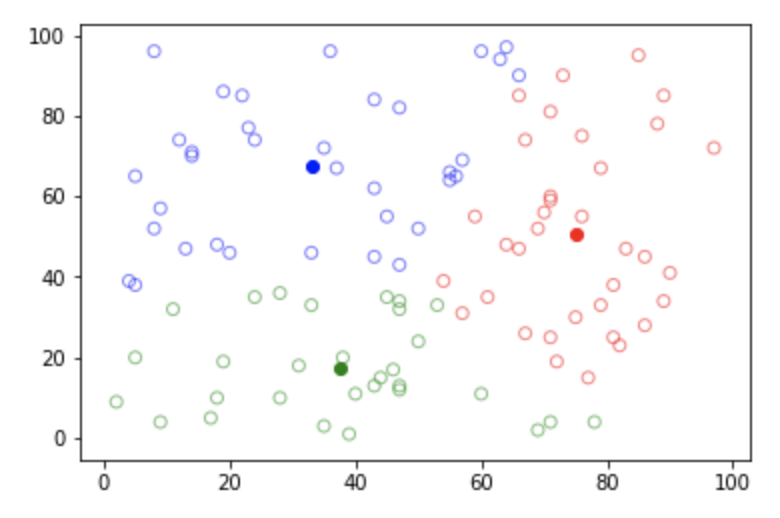
8) 그리기
import matplotlib.pyplot as plt
colorMap = ['r', 'g', 'b', 'k']
for i in range(N):
plt.scatter(data[i][0], data[i][1], facecolor='none', alpha=.5, edgecolor=colorMap[rnk[i].index(max(rnk[i]))])
for i, _ in enumerate(centroid):
plt.scatter(_[0], _[1], color=colorMap[i])
plt.show()

9) 각 점들과 중심간의 거리의 합 구하기
def sse(X, c):
error = 0
for x in X:
error += distance(x, c)
return error
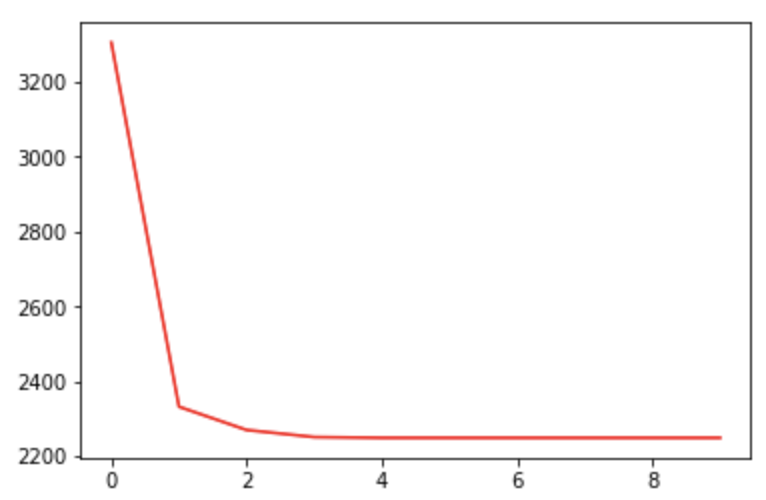
10) 10번 반복하고 오차율 변화 살펴보기
errorRate = list()
for _ in range(10):
rnk = list(list(0 for _ in range(K)) for _ in range(N)) # 빈 공간 생성(각 클러스터에 소속 가능한 갯수만큼 초기값 0
for i in range(N):
j = expectation(data[i], centroid)
rnk[i][j] = 1
_sse = 0
for k in range(K):
X = [data[i] for i in range(N) if rnk[i][k]]
_sse += sse(X, centroid[k])
centroid[k] = maximization(X)
errorRate.append(_sse)
plt.plot(range(10), errorRate, "r-")
plt.show()
11) angle로 할 때 주의사항
- Angle에서는 expectation가 min이 아닌 Max로만 바뀌면 된다.
'데이터 분석가 역량' 카테고리의 다른 글
| day 28 ] 성능평가 (0) | 2019.06.11 |
|---|---|
| Day 27 ] 기사 분류 (0) | 2019.06.10 |
| Day 25 ] Naive Bayes (0) | 2019.06.05 |
| Day 22 ] Classification (0) | 2019.05.30 |
| Day 21 ] Project2 유사도 분석 (0) | 2019.05.29 |
